1. はじめに:関数の苦手意識は「全体像の理解」で克服できる
1-1. そもそも「関数」ってなに?
中学生になると、「関数」という言葉が登場しますが、いきなり難しそうに感じる人も多いのではないでしょうか?
関数とは、ある数(x)を決めると、それに対応して別の数(y)が決まるという関係のことです。
たとえば、パンを1個100円で買う場合、「x=買った個数」「y=支払う金額」とすると、
y = 100x
という関数の式で表せます。逆に言うと、yが決まればxが決まるとも捉えられます。
このように、関数は「変化するものどうしの関係」を表したものなのです。
1-2. なぜ関数が難しく感じるのか?
関数が苦手という中学生は、「何をどう考えればいいのかわからない」という状態になりがちです。具体的には、
- 式を立てるのが苦手
- グラフを描くのが面倒
- 文章問題になると混乱する
こうした悩みは、関数の基本パターンをしっかり押さえていないことが原因であることが多いです。この記事では、まずは一次関数・二次関数の基本から、グラフや文章題の考え方まで丁寧に解説します。
2. 一次関数の基本と解き方
2-1. 一次関数とは?基本の形と意味(y = ax + b)
一次関数とは、xの一次式(1乗の式)でyが表されるものです。
基本の形は、
y = ax + b
ここで、
- a:変化の割合(xが1増えるとyはいくつ増えるか)
- b:切片(x=0のときのyの値)
たとえば「y = 2x + 1」なら、
- xが1増えるごとに、yは2ずつ増える
- xが0のとき、yは1
という関係を表しています。
2-2. 一次関数のグラフの書き方(表の作り方〜グラフ作成)
グラフを書く手順は次のとおりです:
- xにいくつかの値(−2〜2など)を代入して、yの値を求める
- 表にまとめる
- 求めた点を座標平面にプロット
- 点を直線で結ぶ
例:y = 2x + 1 の場合
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | -3 | -1 | 1 | 3 | 5 |
この5点をグラフに書いて直線を引けばOKです。
ここでは丁寧に説明するために5点を書いていますが、直線というのは2点が決まれば書けるので、グラフが通る2点が分かれば一次関数の式が書けるということです。
2-3. 一次関数の問題を解く3ステップ
- 表を作る(xとyの関係を数値で確認)
- グラフを描く(直線の傾きと切片を意識)
- 文章題では式に変換(xとyが何を表しているか明確に)
2-4. よく出るパターン問題とその考え方
- グラフと式の関係を問う問題:y=ax+bの「a」は傾き、「b」は切片と理解して解く
例)このグラフの「傾き」(「変化の割合」)は何ですか? - 2点を通る直線の式を求める問題:変化の割合aを計算 → 点の座標を使ってbを出す
2-5. 点数を取りやすいポイント
- 表は丁寧に作成(計算ミスを防ぐ)
- グラフは目盛りをそろえ、定規を使って正確に描く(図形問題にも役立つ)
- 式に意味を持たせて考える(xとyが何を表すか理解する)
3. 二次関数の基本と解き方
3-1. 二次関数とは?基本の形と意味(y = ax²)
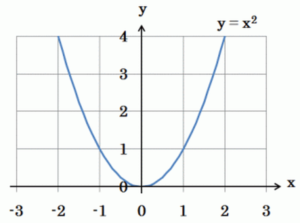
中学で扱う二次関数は、y = ax² という形です。
このグラフは「放物線」と呼ばれる曲線になり、
- aが正(a>0)のときは上に開いたU字型
- aが負(a<0)のときは下に開いた山型
になります。
3-2. 放物線の特徴を知ろう(頂点・軸・対称性)
二次関数のグラフには特徴があります:
- 頂点:グラフの一番低い(または高い)点(x=0のときが頂点になることが多い)
- 軸:左右対称になる線(y軸など)
- 対称性:xの値が左右対称な位置にあるとき、yの値は同じになる
例:y = x² の場合
| x | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| y | 4 | 1 | 0 | 1 | 4 |
左右対称のグラフになります。
3-3. 二次関数のグラフの書き方
- xにいくつかの値を代入して、yを求める
- 表を作成
- 座標をグラフに書いて、なめらかな曲線で結ぶ
※直線ではなく、なだらかな放物線を描くのがポイント。
3-4. 二次関数の文章題の読み取りとアプローチ
- 文章中の「高さ」「距離」「時間」などをxやyに置き換える
- 例:「ボールを投げた高さの変化」→ y=ax²の式で表す
- 与えられた条件から、aの値を決めて式を作成
3-5. 点を取るためのチェックポイント
- グラフの軸・頂点・対称性を丁寧に表す
- 表の数値にミスがないか確認
- 放物線をなめらかに描く練習をする
4. 関数の文章題を解くコツ
4-1. 「変化の割合」を使いこなそう(一次関数)
一次関数では「変化の割合」が超重要。これは「傾き」とも呼ばれます。
変化の割合 = yの増加量 ÷ xの増加量
文章問題でも、「1時間で◯km進む」「1個あたり◯円」など、変化の割合を見つけて式を立てましょう。
4-2. 「対応表」を活用する考え方
xとyの関係を数値で確認したいときは「表」が便利。
対応表を作ることで、どんな変化があるのか、どんな式になりそうか見えてきます。
4-3. 式に置き換える練習方法
文章の中の「〜に比例する」「〜の何倍」「◯個で△円」などを見つけたら、それをxやyに置き換えて式にする練習をしましょう。
例:「1個100円のリンゴをx個買う」→ y = 100x
4-4. 問題文を図や表に「見える化」しよう
文章を読んでもイメージできない場合は、
- 表にまとめる
- 簡単な図を書く
- 関係を線でつなぐ
など、「見える化」することで理解が進みます。
5. 関数問題を解くための学習法と勉強のコツ
5-1. 解き方のパターンを覚えて得点源にする
関数問題には「よく出るパターン」があります。たとえば:
- 表から式を立てる
- グラフから情報を読み取る
- 一次関数と二次関数のグラフの交点を求める
これらは繰り返し練習すれば、確実に点を取れる問題になります。
5-2. グラフを「自分の手で描く」ことの重要性
関数の理解は、グラフを描くことで深まります。
ノートやプリントに何度もグラフを描いて、「目で見て」関係性をつかみましょう。
5-3. ミスしやすいポイントの対策法
- 符号ミス(−が+になっている)
- 計算ミス(2×3=5みたいな初歩的なミス)
- グラフの目盛りミス(ずれてプロット)
→ これらは「見直し」を習慣にすることで防げます。
5-4. 使えるおすすめ問題集や無料教材の紹介
- 学校のワーク(基本問題が充実)
- スタディサプリやTry IT(動画で学べる)
- 教科書準拠の問題集(書店で購入可)
6. おわりに:関数を苦手から「得意」へ変える第一歩
6-1. 最初はゆっくりでも「分かる感覚」を大切に
関数は、慣れるまでは時間がかかります。最初は理解できなくても焦らず、「あ、わかった!」という感覚を大切にして、少しずつ前に進みましょう。
6-2. 練習すれば、関数は「点が取りやすい単元」になる!
関数は最初こそ難しく感じますが、問題のパターンが決まっているので、覚えて練習すれば点が取りやすいです。
苦手意識を少しずつなくして、「関数=得意!」と言えるようになりましょう!


コメント